java (7) spring (1)

[ JAVA ] Arrays.sort()의 내부 동작(2)

- Timsort

Posted by 자바니또 on January 06, 2021 · 4 mins read

개요

저번 포스팅에서는 원시타입(Primitive type)배열을 정렬할 때 사용되는 자바의 기본정렬인 DualPivotQuicksort.sort()에 대해 알아보았다. 이번엔 Object타입의 배열을 정렬할 때 사용되는 TimSort.sort()를 알아보자.

 

java.util.Arrays.sort(:Object[])

img7

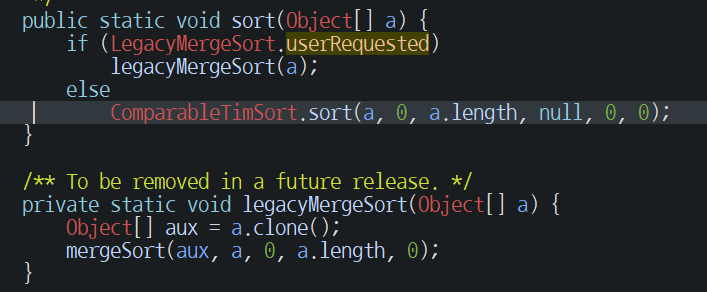
String 배열을 인자로 Arrays.sort()를 호출했을 때 불려지는 메서드이다. LegacyMergeSort()와 ComparableTimSort.sort()가 분기되어있다. 바로 밑에 LegacyMergeSort가 있는데 주석을 보면 이 후 버전에서는 삭제될 것이라고 쓰여있다. java 7부터는 별도로 설정하지 않는 경우 TimSort만 적용된다.

 

왜 java는 TimSort를 선택했을까?

TimSort는 실 세계의 데이터가 대략 정렬된 상태로 있는 경우가 많다는 경험에서 기반하여 디자인된 알고리즘이며, 병합 정렬 및 삽입정렬에서 파생 된 안정적인 하이브리드 정렬이다. 동시에 입력배열의 사이즈가 작으면 알고리즘을 다르게하는 적응적 알고리즘이다.

img6

위의 이미지는 java.util.Arrays의 sort(Object[])에 대한 메서드에 대한 공식문서이다. 중요한 부분만 해석해보면

  • 배열의 모든 요소는 Comparable인터페이스를 구현해야하고 서로 비교할 수 있어야합니다.(즉, e1.compareTo(e2)는 ClassCastException을 발생시키지 않아야 합니다.)

  • 이 정렬은 안정적인 정렬입니다.

  • 구현 참고 사항 : 이 구현은 입력배열이 부분적으로 정렬이 되어있을 때 NlogN보다 훨씬 적은 수의 비교를 필요로하는 안정적이고, 적응적이며, 반복적인 병합정렬이다.

  • 입력배열이 무작위로 정렬 될 때는 기존 병합정렬의 성능인 O(NlogN)을 보장합니다.

  • 입력배열이 거의 정렬 된 경우 구현에는 약 N번의 비교가 필요합니다.

  • 이 정렬은 둘 이상의 정렬된 배열을 병합하는 데 적합합니다.

Comparable인터페이스를 구현하면 compare() 오버라이드를 강제하는데, 이것은 사용자 오브젝트끼리 비교를 할 때 무엇을 비교하여 정렬할 지 정의하는 메서드라고만 알고 넘어가자. 더 자세한 설명은 다음 포스팅으로 미루도록 하겠다.

결론 적으로 TimSort는 이미 정렬되어 있는 입력을 받는 최상의 경우의 성능은 O(N)이고, 평균적인 성능과 하나도 정렬되지 않은 입력을 받는 최악의 경우의 성능조차 O(NlogN)를 보장하는 매우 빠른 알고리즘이다. 부분 적으로 정렬되어 있는 경우에는 실제로 O(NlogN)보다 빠른 성능을 보여준다. 결코 느리지 않은 MergeSort보다도 훨씬 빠르기에 선택하지 않을 이유가 없다.

 

TimSort

TimSort의 동작방식에 대해서 핵심만 간략히 짚고 넘어가자.

img8

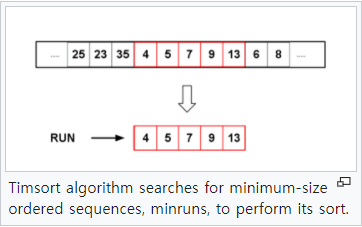
절반 씩 분할하는 MergeSort와 달리 TimSort에서는 Run이라는 동적인 단위로 입력배열을 나눈다. 입력된 데이터들 중 미리 정렬되어있거나 역순으로 정렬되어있는 Sequence를 기본단위로 해서 Run을 뽑아낸다. 이때 뽑아낸 run의 크기가 미리 정해놓은 최소 크기인 minrun보다 작다면 minrun만큼의 구간을 binarySort()를 수행하여 빠르게 정렬하고 run으로 잡는다.

binarySort()는 이진삽입정렬로서 짧은 sequence에 대해서 매우 빠른 성능을 가지는 알고리즘이다. (minrun의 크기는 보통 32 or 64 처럼 2의 거듭제곱으로 하며 이유는 병합할 때 효율적이기 때문이다.)

img9

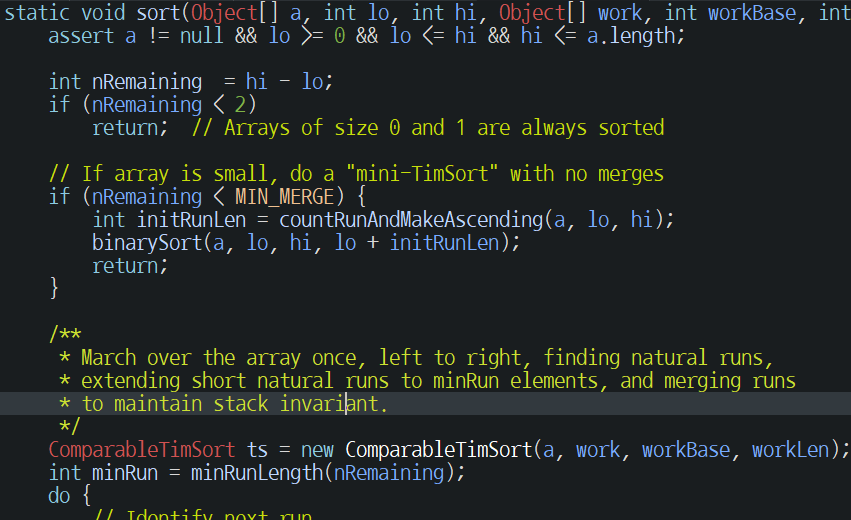
TimSort가 수행되면 입력된 배열의 크기를 확인하고 작다면 바로 이진삽입정렬로 정렬 후 리턴해버린다. (작음의 기준값인 MIN_MERGE는 JAVA에서는 64로 설정되어 있다._11기준) 충분히 크다면 minRunLength()를 통해 minrun의 크기를 정한다.

img10

이렇게 만들어진 Run들은 길이와 시작점으로 이루어진 구조체인 merge_stack에 쌓으면서 중간중간 병합을 한다. stack에 쌓고 병합을 하는 이유는 정렬의 효율을 높여주는 안정성을 유지하기 위해서이다. 안정성을 유지하기 위해서는 인접한 run끼리 병합을 수행해야하고 그 때문에 stack을 사용한다. (자세한 내용은 문서를 참고하기 바란다.)

병합은 스택의 run들의 상태를 다음과 같이 유지하기 위해서 필요할 때 마다 수행한다.

1. |Z| > |Y| + |X|
2. |Y| > |X|

 

정리

  • TimSort는 실 세계의 데이터가 대략 정렬된 상태로 있는 경우가 많다는 경험에서 기반하여 디자인된 알고리즘으로서, 어느정도 정렬이 된 sequence에서 매우 좋은 성능을 보인다.

  • 거의 다 정렬되어 있는 sequence에 대해서는 O(N)의 성능을 보인다.

  • 부분적으로 정렬되어 있는 sequence에 대해서는 O(NlogN) 이상의 성능을 보인다.

  • 정렬되어있지 않는 sequence에 대해서도 O(NlogN)의 성능을 보장한다.

  • TimSort는 stable하고 adaptive한 hybrid 알고리즘이다.

 

Reference

← Previous Post Next Post →